DÉNOMBREMENT (IDÉE DE)

DÉNOMBREMENT (IDÉE DE)

Le mot « dénombrement » est le nom donné à une certaine opération qui, comme toute opération, présuppose les deux termes d’une distinction: l’action elle-même de dénombrer et la réalité sur laquelle elle s’exerce. Il y a le dénombrant d’une part, le dénombré d’autre part. Distinction qu’il convient de situer à deux niveaux, celui de l’expérience la plus concrète et celui de la théorie pure, étant bien entendu que, comme pour la plupart des notions mathématiques, c’est par le passage d’un niveau à l’autre que l’on enrichit la science et rationalise l’action.

Le dénombrement du point de vue empirique

Rien n’est, en pareil cas, plus suggestif que la lecture de quelques dictionnaires ou lexiques français-anglais, français-allemand, français-italien, etc., et d’y regarder par quels mots est traduit le mot français «dénombrement»; sans qu’il soit nécessaire d’aller jusqu’à l’étude exhaustive et systématique que devrait faire un linguiste, on voit pourtant apparaître le noyau sémantique de la notion et le nuage de concepts voisins qu’elle appelle. Un examen analogue est à faire aussi sur les lexiques, dictionnaires ou encyclopédies, en langue française exclusivement, mais édités à des époques diverses.

L’action de dénombrer apparaît surtout comme très voisine de celle de compter ; les objets comptés étant des personnes ou des objets matériels, notamment des «biens», au sens économique du terme. «Voici le dénombrement des fils de Sem, Cham et Japhet, enfants de Noé», évoque Littré citant la Genèse. Quant aux choses, le mot dénombrement, d’un emploi courant pour les situations d’héritage, a pu devenir un terme de «fief»; on comprend bien pourquoi, le vassal devant faire une déclaration écrite de tous les droits qu’il tenait de son seigneur. Les mots cens, census, recensement sont, avec leur connotation militaire ou électorale, de très proches voisins sémantiques de dénombrement. De dénombrer et compter, on passe facilement à calculer. Si les Anglo-Saxons mettent surtout l’accent sur «comptage» et «census», les Italiens vont davantage sur les termes évoquant la compilation ; curieusement, l’idée du «dépouillement des données» glisse vers un sens moins noble, celui du dépouillement lors d’un pillage, d’un vol. La langue allemande enfin, qui traduit le plus souvent le mot français «dépouillement» par Aufzählung , exprime une idée proche parente avec Erhebung , c’est-à-dire «enquête», «recherche», «investigation» et aussi «levée» (au sens militaire de «levée de contingents de conscrits»), et surtout avec Erfassung qui, toujours dans le langage de l’administration militaire, signifie «enregistrement» ou «recensement».

Compter, recenser, compiler, enregistrer, telles sont les opérations concrètes les plus fréquemment évoquées qui, toujours sur le plan concret, préparent ou même constituent l’opération de dénombrement. Si l’on passe de l’opération à l’objet sur lequel on opère, la plus grande diversité apparaît aux théoriciens comme aux praticiens: des offres, des biens immobiliers que l’on recense, des pièces de monnaie que l’avare compte avec soin et passion, des moutons que compte le berger, etc. Même des objets purement abstraits peuvent être dénombrés, comme en témoigne le célèbre texte de Descartes: «... faire partout des dénombrements si entiers et des revues si générales que je fusse assuré de ne rien omettre». À cet égard, il est intéressant de noter également que le mot allemand fassen (nous parlions tout à l’heure de l’Erfassung ) a les significations concrètes de «saisir», «empoigner», «prendre», mais aussi les significations abstraites de «saisir» (intellectuellement) et de «comprendre». Ces considérations rendent naturel le passage de la notion de dénombrement comme opération concrète à celle de dénombrement comme concept théorique.

Le glissement à la notion d’ensemble est en effet facile. Si, avec Cantor, on appelle ensemble le «groupement en un tout d’objets bien définis, et discernables de notre perception ou de notre entendement, que nous appelons les éléments de l’ensemble», les deux notions permettant de caractériser un ensemble se retrouvent dans les exemples concrets évoqués: la propriété qui, attribuable à chaque élément de l’ensemble, en permet la définition, et le nombre de ces éléments. Faire un recensement des jeunes gens susceptibles d’être incorporés dans une formation militaire, c’est bien, implicitement ou explicitement, avoir d’abord défini l’ensemble en l’occurrence intéressant par les propriétés de sexe, d’âge, d’appartenance à une région géographique précisément délimitée, etc., afin de pouvoir les compter, c’est-à-dire trouver le nombre des sujets dont on pourra faire des conscrits. Dresser la liste des livres et articles de revues ou de journaux publiés par un auteur dont la plume fut féconde, c’est délimiter l’ensemble par la définition de l’écrivain ou par sa simple dénomination, et se donner le moyen de compter le nombre de livres, le nombre d’articles, et par conséquent la somme des deux. Le dénombrement porte sur les éléments de l’ensemble, les objets dénombrés sont considérés seulement sous l’aspect de leur appartenance à l’ensemble.

Mais comme les éléments ne peuvent être dénombrés que si l’ensemble est dénombrable , il importe, si l’on veut bien comprendre l’opération théorique dite dénombrement , d’entrer un peu plus avant dans la théorie des ensembles. Auparavant, quelques remarques s’imposent, car d’autres notions mathématiques se trouvent comme en germe dans les divers emplois empiriques suggérés par les dictionnaires et lexiques.

Le dénombrement, opération empirique, est inséparable de deux autres actes mentaux; la saisie des grands nombres et le classement des objets à dénombrer. On peut compter le nombre de bonbons de chocolat que l’on trouve dans une boîte que l’on a payée cher sans bien savoir si le prix était dû au nombre de bonbons ou à la belle décoration de leur emballage, on ne dira pas qu’on les a dénombrés . Certes ni l’idée exprimée ni l’expression elle-même ne serait incorrecte – mais l’usage a fait prévaloir une signification du mot «dénombrement» qui réfère à la prise de conscience du nombre exact ou au moins approximatif des éléments d’un ensemble très nombreux, trop nombreux pour qu’on puisse l’estimer sans un coup d’œil exercé ou sans quelque opération préalable. L’administrateur municipal peut savoir qu’il y a de nombreux jeunes gens dans le ressort dont il a la responsabilité, mais il lui faudra les dénombrer pour répondre à une demande du ministre des Armées ou du ministre des Finances: il lui faudra donc d’abord classer ces effectifs par exemple en classes d’âge ou selon le sexe ou le niveau socio-économique. Le lien entre les notions de «grands nombres» et de «classement» est, dans ce contexte, évident: c’est parce qu’il ne peut pas saisir immédiatement et d’un seul coup d’œil un nombre même grossièrement approximatif que l’administrateur divise en classes son effectif pour rendre plus aisé et même tout simplement faisable le décompte des éléments de chacune des classes. On voit ainsi comment et pourquoi la notion de dénombrement est à l’origine de la statistique descriptive , branche de cette science par laquelle on apprend à dominer les grands nombres, ainsi que de la démographie .

Du concret à l’abstrait

Comme les notions d’«ensemble» et de «classe», celle de «population» se caractérise par la définition (on aurait autrefois parlé de sa «compréhension») et par le nombre des sujets qui la composent (l’«extension» correspondant à la «compréhension»). Or il est manifestement absurde de parler d’une population d’ingénieurs électroniciens dont l’effectif serait égal à 4 625,37: un effectif d’une population est nécessairement un nombre entier. Le service des impôts dénombre les citoyens imposables, les bureaux de recrutement dénombrent les sujets qui ont l’âge légal du service militaire, le ministère des Universités dénombre les étudiants entrant ou sortant des établissements de son ressort..., même si son évaluation est difficile à faire, l’effectif chaque fois considéré ne peut pas ne pas être un nombre entier. L’examen de ces opérations empiriques suggère une première conclusion, peut-être suspecte: le dénombrement d’une population, d’un ensemble, d’une collection ne serait possible qu’à la condition que les éléments soient dénombrables. Mais «dénombrable» signifie-t-il «n’être exprimable que par un nombre entier»? Pour y répondre, il nous faut maintenant passer du plan empirique au plan théorique pur.

Le dénombrable

Le lecteur peu habitué aux mathématiques supérieures peut être ici gêné par une confusion que saura éviter l’expert. S’agissant de nombres entiers, rien n’est à craindre si les éléments de l’ensemble considéré sont des objets concrets ou même abstraits, mais non numériques; en revanche, il y a risque d’incompréhension si ces éléments sont eux-mêmes des nombres. Les deux ensembles E¹ =a, b, c, d, e et E² =1, 2, 3, 4, 5 ont même nombre d’éléments; on dit alors que le «cardinal» de E¹ est égal au «cardinal» de E², c’est-à-dire à 5. C’est seulement pour E² que la notion de nombre entier joue à deux niveaux: 5 est un des éléments, 5 est aussi le nombre des éléments de l’ensemble.

Cela dit, comment caractériser les ensembles dénombrables ? Pour y parvenir, il nous faut passer par les notions d’égalité et d’équivalence, d’une part, par la distinction entre ensemble fini et ensemble infini, d’autre part, et mobiliser les opérations élémentaires sur les ensembles (l’inclusion essentiellement).

Premièrement, deux ensembles sont équivalents si à chaque élément de l’un correspond un élément et un seul de l’autre, et réciproquement, c’est-à-dire s’ils sont en correspondance biunivoque. L’ensemble des élèves d’une classe et l’ensemble des chaises sur lesquelles ils sont assis sont des ensembles équivalents. Mais, comme on va voir, l’équivalence se distingue de l’égalité. Intuitivement, on voit tout de suite que l’ensemble ¹ des nombres entiers ¹ =1, 2, 3, 4, ... est un ensemble infini , c’est-à-dire ayant un nombre infini d’éléments, chacun étant un nombre entier, tandis que les ensembles E¹ et E² mentionnés plus haut étaient deux ensembles finis, égaux entre eux car ayant le même cardinal. Intuitivement, on voit non moins vite que l’ensemble des nombres entiers pairs ² =2, 4, 6, 8, ... est aussi un ensemble infini . Toujours au niveau de l’intuition, on est tenté de dire que ¹ et ² ne sont pas égaux entre eux, car on a manifestement ² 說 ¹, l’ensemble ¹ comportant tous les éléments de ², mais aussi tous les nombres impairs. En revanche, ¹ et ² sont équivalents, comme on le voit en écrivant:

Même en allant à cet infini indiqué par les points de suspension, à chaque élément de ¹ correspond un élément de ² et un seul. Aussi comprend-on la distinction faite par Dedekind entre ensemble fini et ensemble infini, à partir des notions comparées d’égalité et d’équivalence: «S’il existe un sous-ensemble de ¹ équivalent à ¹, ¹ est un ensemble infini.» Ici ² est un sous-ensemble de ¹ équivalent à ¹. Mais alors qu’en est-il du nombre des éléments de ¹, comparé au nombre des éléments de ²? ¹ et ² ont le même cardinal puisqu’ils sont équivalents, mais ce nombre cardinal est un nombre qu’on appellera transfini et désignera par 尿 (aleph); nous pourrons dire alors avec Breuer: «Nous appelons ensembles dénombrables des ensembles de puissance 尿. Les ensembles dénombrables sont donc des ensembles pour lesquels on peut réaliser une application sur l’ensemble des nombres naturels, en d’autres termes, dont les éléments peuvent être ordonnés en une suite; ils ont un premier élément, un deuxième, un troisième, etc.»

Si un ensemble est dénombrable, il y a lieu de démontrer qu’il l’est. Soit par exemple l’ensemble des nombres premiers, qu’on appellera ³. On sait déjà qu’il est infini, car on peut toujours trouver un nombre premier plus grand que celui qu’on a sous les yeux, quelque grand que soit celui-ci: Euclide l’a démontré. Comme d’autre part on peut les ranger en une suite comme on le fit plus haut pour E², on peut toujours écrire: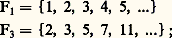

l’ensemble ³ est donc dénombrable.

Tous les ensembles dénombrables, par exemple l’ensemble des entiers, l’ensemble des nombres rationnels, l’ensemble des nombres algébriques, sont équivalents entre eux, ils ont le même cardinal: aleph.

Mais il est des ensembles qui ne sont pas dénombrables, qui sont cependant équivalents les uns aux autres et ont, de ce fait, un autre cardinal que aleph et habituellement désigné par 暈: citons l’ensemble des nombres réels compris entre 0 et 1, l’ensemble des nombres réels compris entre moins l’infini et plus l’infini, l’ensemble des points d’un segment, celui des points d’une droite, celui des points d’une demi-droite: ils ont la «puissance du continu»: les étudier serait hors de l’actuel propos, mais la notion de «dénombrable» ne se comprend bien que si l’on évoque aussi les ensembles qui ne le sont pas.

Encyclopédie Universelle. 2012.